반응형
목차
1. 지식 표현(Knowledge Representation)
2. 의미망
3. 프레임
4. 논리(Logic)
5. 명제 논리
6. 술어 논리
7. 술어 논리에서 추론
8. 프롤로그(prolog)
1. 지식 표현(Knowledge Representation)
- 지식 표현 방법의 종류
- 생성 규칙(Production Rule) 또는 규칙
- 절차적(procedural)
- 술어 논리(Predicate Logic)
- 선언적(declarative)
- 의미망(Semantic Net)
- 선언적(declarative)
- 프레임(frame)
- 선언적(declarative)
- 생성 규칙(Production Rule) 또는 규칙
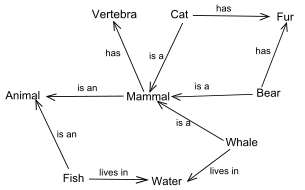
2. 의미망(Semantic Network)
- 의미망(semantic network)은 방향 그래프를 이용하여 개념 간의 관계를 나타내는 방법이다.
- 그래프는 노드와 간선으로 이루어진다.
- 노드는 사물(object), 개념(concepts) 등을 표현한다.
- 간선(edge)는 사물이나 개념 사이의 관계이다.
- 노드 사이의 간선은 "...의 일종이다"(is-a), "...을 가지고 있다"('has), "...은 하나의 예이다."(inst-of)와 같은 관계를 나타낸다.
- 의미망은 매우 복잡한 개념이나 인과 관계를 잘 표현할 수 있지만 지식의 양이 커지면 너무 복잡해져서 조작이 어렵다는 단점도 가지고 있다.
- 의미망을 위한 표준 지침이 없기 때문에 시스템에 따라 의미망의 형태가 다를 수 있다.
3. 프레임
- 프레임
- 프레임(frame)은 1970년대에 Marvin Minsky가 제안한 지식 표현 방법으로 의미망에서 파생되었다.
- 프레임은 특정 객체와 그 속성을 묶어서 하나로 조직화하는 개념이며 개념, 객체, 상황들을 기술하는 데 유리하다.
-
- 프레임은 객체의 속성과 값으로 이루어져 있다.
- 개개의 속성은 슬롯(slot)이라고 불리고 슬롯은 값을 가질 수가 있다.
- 프레임은 프로그래밍 언어의 구조체나 객체(object)와 유사하며 객체의 필드에 해당하는 것은 슬롯이다.
-
- 프로시저
- "if-added" 프로시져는 새로운 정보가 그 슬롯에 추가되어야 할 때 실행된다.
- "if-deleted" 프로시져는 어떤 값이 슬롯으로부터 제거될 때 실행된다. 이 변경에 따라 다른 슬롯의 값도 변경할 필요가 있을 것이다.
- "if-needed" 프로시져는 빈 슬롯에 어떤 값이 필요해질 때에 실행된다.
- 프레임과 객체 지향 프로그래밍
- 인공지능 분야에서는 프레임이란 용어로 객체를 나타낸다.
- 객체의 필드에 해당하는 것이 프레임의 슬롯이다.
- 프레임의 슬롯은 값뿐만 아니라 프로시저도 가질 수 있다. 슬롯에 붙은 프로시저가 바로 객체의 메소드라고 볼 수 있다.
- 프레임과 상속
- 프레임도 인스턴스 프레임(instance frame)과 클래스 프레임(class frame)로 나눌 수 있다.
-
- 프레임도 인스턴스 프레임(instance frame)과 클래스 프레임(class frame)로 나눌 수 있다.
4. 논리(Logic)
- 전통적인 논리
- 명제 논리
- 1차 술어 논리
- 2차 술어 논리
- 인공지능에서 많이 사용하는 논리는 명제 논리, 1차 술어 논리이다.
- 술어 논리
- 예를 들어보자. "만약 x가 새라면, x는 날개를 가질 것이다"라는 규칙이 있다고 하자.
- (∀x){is_a(x, Bird) →has(x,Wings)}
- 장점
- 수학적인 근거를 바탕으로 논리 개념을 자연스럽게 표현할 수 있다.
- 지식의 정형화 영역에 적합하다. 예를 들어서 정리 증명(theorem proving) 기법을 사용할 수 있다.
- 지식의 첨가와 삭제가 용이하고 비교적 단순하다.
- 단점
- 절차적인 지식 표현이 어렵다.
- 사실의 구성 법칙이 부족하므로 실세계의 복잡한 구조를 표현하기 어렵다.
- 문장으로 논리적인 관계를 표현하기 때문에 그렇다.
- 예를 들어보자. "만약 x가 새라면, x는 날개를 가질 것이다"라는 규칙이 있다고 하자.
5. 명제 논리
- 명제 논리: 각각의 문장이라고 보면 된다.
- 기호 논리학에서 명제(proposition)는 참(true, T)이거나 또는 거짓(false, F)을 판별할 수 있는 문장이다.
- P = 마트는 월요일부터 토요일까지 영업한다.
- Q = 오늘은 일요일이다.
- R = 오늘 마트는 영업하지 않는다.
- 논리 연산자 사용 가능
- Q = 오늘은 일요일이다.
- NOT Q = 오늘은 일요일이 아니다.
- J = 옷은 파랑색이다.
- K = 옷은 스트라이프 무니가 있다.
- "L = J AND K" = 옷은 파랑색이고 스트라이프 무늬가 있다.
- Model
- (P: true, Q: false)
- "P는 참이고 Q는 거짓이다"라고 표현하는 것 자체가 모델이다.
- 기호 논리학에서 명제(proposition)는 참(true, T)이거나 또는 거짓(false, F)을 판별할 수 있는 문장이다.
- 함축(→, Implication)
- C = 오늘은 휴일이다.
- D = 오늘은 수업이 없다.
- E = C → D
- 복합 명제의 논리표
-

- A가 F일 때 A → B가 참인 이유
- (논리적 동치)(if)A → (then)B ≡ ¬A ∨(or) B 이다. A가 F이면 ¬A는 T이다. 따라서 (if)A → (then)B(≡¬A ∨(or) B)는 T이다.(Implication Elimination. 출처: https://en.wikipedia.org/wiki/Logical_equivalence)
-

- (집합적 설명)A라는 명제가 있고 사실이 A가 거짓이면 A는 공집합이다. 공집합은 모든 집합의 부분집합이다. B는 집합이다. 따라서 A(공집합)는 B의 부분집합이다. 따라서 참이다.
- p이면 q에서 가정, 전제가 거짓일 때 조건문이 항상 참인 이유
-
- 명제 논리에서의 추론
- 추론(inference): 가지고 있는 지식과 알고 있는 사실로부터 새로운 사실을 유추하여 내는 것
- (지식, Knowledge Base) 우리집 강아지는 집 안에 있거나 앞마당에 있다.(A or B)
- (사실) 강아지가 집 안에 없다.(not A이다. A가 거짓이라는 말이 아니다.)
- ===================================
- (추론된 사실) 따라서 강아지는 앞마당에 있을 것이다.
- 추론(inference): 가지고 있는 지식과 알고 있는 사실로부터 새로운 사실을 유추하여 내는 것
- 함의(Entailment)
- 모든 모델에서 포함된 문장 α가 사실이면 β도 반드시 사실이다.
- α ⊨ β
- 논리학에서 기호 ⊨는 이중 턴스틸(double turnstile)이라 불리는 기호이다. 그 외에도 이 기호는 '수반하다', '모델이다'라고도 하며 이는 의미론적으로 다음 결과를 수반한다 또는 더 강한 조건이다(is stronger than)임을 의미한다. 이 기호는 중간에 가로선이 하나만 있는 턴스틸 기호(⊢)와 관련이 있으며, 턴스틸이 "구문론"적 관점에서의 연관성을 드러내는 반면 이중 턴스틸은 "의미론적" 관점에서 연관성을 드러낸다.(출처: 위키피디아)
- α ⊨ β
- 추론
- 궁극적으로 가지고 있는 지식 베이스(KB)로부터 Entailment한 α를 찾아내는 과정
- 수식적 표현
- Does KB ⊨ α ? where α is a query.
- 지식베이스가 참일 때 반드시 참인 α를 찾는 과정이다.
- 만약, 모든 모델에서 KB가 사실이면, α가 사실이고 이는 KB가 α를 수반(entail)한다. → 모델 체킹(model checking) 알고리즘의 근거
- 모든 모델에서 포함된 문장 α가 사실이면 β도 반드시 사실이다.
- 추론 법칙
- 모더스 포넌스(Modus Ponens)
- "---------------"선을 경계로, 위에는 "전제 조건"과 "전제 조건에 관련된 사실"을 놓는다. 선 아래에는 "전제 조건"과 "전제 조건에 관련된 사실"로부터 나타나는 "결론"을 표시한다. 모더스 포넌스는 이런 방법으로 숨겨진 진실을 추론하는 방법이다.
- 방법
- 규칙 | A → B
- 사실 | A
- ---------------
- 결론 B
- 예제
- "홍길동이 세계 일주 중이라면 → 로또에 당첨된 것이다"
- "홍길동은 세계 일주 중이다."
- --------------------------------------------------------------
- ∴ "홍길동은 로또에 당첨된 것이다."
- 방법
- 모더스 톨렌스(Modus Tollens, 부정 논법)
- 방법
- 규칙 | A → B
- 사실 | NOT B
- --------------
- 결론 NOT A
- 예제
- "어떤 동물이 강아지라면 → 어떤 동물은 4개의 다리를 가지고 있다."
- "어떤 동물은 4개의 다리를 가지고 있지 않다."
- ---------------------------------------------------------------------------
- ∴ "어떤 동물은 강아지가 아니다."
- 방법
- 삼단 논법
- 방법
- 규칙 | A → B
- 사실 | B → C
- --------------
- 결론 A → C
- 예제
- "소크라테스는 인간이다"
- "인간은 모두 죽는다"
- ---------------------------
- ∴ "소크라테스는 죽는다"
- 방법
- AND Elimination
- AND 조건을 없애는 방법이다. AND로 엮인 여러 사실이 있을 때, 하나의 사실이라는 명제를 추출하는 방법이다.(출처)
- 이는 한 형식에서 다른 형식으로 정보를 변환하는 데 사용하는 추론 규칙이다.
-

- Double Negation Elimination
- 부정의 부정을 제거하는 방법이다. 부정의 부정은 긍정이다를 의미한다.
- ¬(¬A) ≡ A
- Implication Elimination
- A → B ≡ ¬A ∨ B
- A → B에서 →(함축)을 제거하는 방법이다. 두 가지 방법이 있다.
- A → B 에서 A라는 사실을 가져와 B를 생성해낸다.
- 비가 오면 습할 것이다.(조건)
- 비가 온다.(참)
- --------------------------
- 습하다.(참)
-

- 논리적 동치를 사용하여 →를 ∨로 바꾼다.
- 비가 오면 습할 것이다.(조건)
- 비가 오지 않거나 비가 올 것이다.(참)
- --------------------------
- 비가 오지 않거나 (비가 와)습할 것이다.(참)
- A → B 에서 A라는 사실을 가져와 B를 생성해낸다.
-

- Biconditional Elimination
- A ↔ B ≡ (A → B) ^ (B → A)
- 지금까지의 것들은 화살표들을 and 나 or 로 바꾸기 위해 필요한 논리들이다.
- 드모르간의 법칙(De Morgan's Law)
- 집합으로 생각하자
- ¬(A^B) ≡ ¬A ∨ ¬B
- ¬(A∨B) ≡ ¬A ^ ¬B
- 분배 법칙(Distributive Law)
- 집합으로 생각하자
- A ^ (B ∨ C) = (A ^ B) ∨ (A ^ C)
- A ∨ (B ^ C) = (A ∨ B) ^ (A ∨ C)
- Complementary Literal
- A ∨ B(참)
- ¬A(참)
- ====
- B(참)
- Advanced Complementary Literal
- A ∨ B(참)
- ¬B ∨ C(참)
- ======
- A ∨ C(참)
- Conjunctive Normal Form(CNF)
- clauses(∨로 연결된 문장)들이 ^로 연결된 논리적 문장(logical sentence)
- 예: (A ∨ B ∨ C) ^ (D ∨ ¬E) ^ (F ∨ G)
- CNF로의 변환 방법
- ↔(biconditional)을 제거한다.
- A ↔ B ≡ (A → B) ^ (B → A)
- →(implication)을 제거한다.
- A → B ≡ ¬A ∨ B
- ¬(negation, 부정)을 식의 안으로 이동한다.(드모르간의 법칙 이용)
- ¬(A^B) ≡ ¬A ∨ ¬B
- ¬(A∨B) ≡ ¬A ^ ¬B
- 분배법칙을 이용하여 clauses 내부를 ∨로 바꾸어준다.
- A ^ (B ∨ C) = (A ^ B) ∨ (A ^ C)
- A ∨ (B ^ C) = (A ∨ B) ^ (A ∨ C)
- ↔(biconditional)을 제거한다.
- 예
- (A ∨ B) → C
- ¬(A ∨ B) ∨ C (함축 제거)
- (¬A ^ ¬B) ∨ C (드모르간의 법칙)
- (¬A ∨ C) ^ (¬B ∨ C) (분배법칙)
- 이렇게 하는 이유는 새로운 명제를 생성해낼 수 있기 때문이다.
- ¬A ∨ C
- ¬B ∨ C
- ======
- ¬A ∨ ¬B
- clauses(∨로 연결된 문장)들이 ^로 연결된 논리적 문장(logical sentence)
- Inference by Resolution
- General Proof
- Example of Proof by Resolution
6. 술어 논리
- 술어(predicate) 논리
- Constant symbols: objects
- Predicate Sumbols: 개별 상수의 참(true) 또는 거짓(false)을 보유할 수 있는 속성
- 명제 논리에서 하나의 명제가 나누어질 수 없기 때문에 어려움이 있다. → 즉 우리는 전체 명제가 참이냐 거짓이냐만을 알 수 있다.
- 예를 들어서 "신호등이 파랑색이다."라는 명제가 있다면 이것을 "신호등"과 "파랑색이다"로 나눌 수 있다면 아주 편리할 것이다.
- 술어 논리에서는 하나의 명제가 객체(object, 또는 인수)와 술어(predicate)로 나누어진다.
- 변수와 한정자를 사용할 수 있다.
- 이와 같은 술어 논리의 특징 때문에 명제를 사용하는 것보다, 훨씬 더 구체적으로 지식을 표현할 수 있다.
- 술어 논리의 예
- 명제 논리: Kim has a house
- 술어 논리: HAS(Kim, house)
- 명제 논리: The orange is yellow
- 술어 논리: YELLOW(orange)
- 객체와 관계
- 객체는 상수 기호로 나타낸다: 바둑이, 야옹이, Richard, ...
- 관계는 술어 기호로 나타낸다: HUMAN, DOG, CAT, HAT, ...
- 변수
- 예를 들어서 "x가 인간이라면"은 다음과 같이 표현할 수 있다.
- HUMAN(x)
- x가 인간이라면 위의 술어 논리식은 참이 된다.
- 예를 들어서 "x가 인간이라면"은 다음과 같이 표현할 수 있다.
- 한정사
- 한정사는 변수의 범위를 서술하는 기호이다.
- 술어 논리에서는 전칭 한정사(universal quantifier) ∀와 존재 한정사(existential quantifier) ∃를 사용할 수 있다.
- 전칭 한정사 ∀는 "모든"이라는 의미이다.
- All dog like cats
- ∀x [DOG(x) → LIKES(x, cat)]
- 존재 한정사 ∃는 "적어도 하나는 존재"한다는 의미이다.
- Some dog like cats.
- ∃x [DOG(x) → LIKE(x, cat)]
- 전칭 한정사 ∀는 "모든"이라는 의미이다.
- 전칭 인스턴스화(Universal Instantiation)
- All dog like cats
- ∀x [DOG(x) → LIKES(x, cat)]
- 존재 인스턴스화(Existential Instantiation)
- Some dog like cats.
- ∃x [DOG(x) → LIKE(x, cat)]
- 스콜렘 상수: 위 조건을 만족하는 상수(예: x, cat 등)
7. 술어 논리에서 추론
- 술어 논리에서의 추론
- 첫 번째 방법은 술어 논리식을 명제 논리식으로 변환한 후에 명제 논리의 추론 기법을 적용하는 것
- 명제 논리식으로 변환하는 것이 어렵기 때문에 잘 사용하지 않는다.
- 두 번째 방법은 도출(resolution)이다.
- 명제 논리: Kim has a house
- 술어 논리: HAS(Kim, house)
- 명제 논리: The orange is yellow
- 술어 논리: YELLOW(orange)
- 첫 번째 방법은 술어 논리식을 명제 논리식으로 변환한 후에 명제 논리의 추론 기법을 적용하는 것
- 정형식
- 우리가 도출을 사용하려면 모든 지식이 정형식(well-formed formula)으로 표현되어야 한다.
- 기초 공식은 정형식이다.
- P와 Q가 정형식이면 ¬P(¬: 부정, not), P∨Q(∨: 논리합, or), P∧Q(∧: 논리곱, and), P→Q(→: 실질 함축, if P then Q)도 정형식이다.
- P가 정형식이면 ∀x P(x)와 ∃x P(x)도 정형식이다.
- 정형식은 위의 규칙을 반복하여서 형성 가능하다.
-

- 도출은 리터럴과 부정 리터럴을 가지고 있는 2개의 절을 조합하여서 새로운 절을 생성하는 방법이다.
- 도출로 모너스 포넌스를 유도
- 우리가 도출을 사용하려면 모든 지식이 정형식(well-formed formula)으로 표현되어야 한다.
- 도출을 사용하려면
- 도출 기법으로 증명하려면 모든 논리식들을 논리곱 표준형(CNF: Conjunctive Normal Form)으로 바꾸어야 한다.
- 모든 전칭 한정사(Universal Quantifier)는 없앤다(기본적으로 가정된다).
- 존재 한정사(Existential Quantifier)는 스콜렘 함수라고 하는 것으로 바꾼다.
- CNF로 변환하기
- 함축(implication) 기호 →를 제거한다.
- 부정 기호를 기초 공식 안으로 이동한다. 드모르간의 법칙을 이용하여 부정의 범위를 줄인다.
- 전칭 한정사 변수의 이름을 다르게 변경한다.
- 존재 한정사에 의하여 한정되는 변수를 함수로 대체하고 존재 한정사를 제거한다.
- 모든 전칭 한정사를 생략하고, 논리곱 정규형으로 변환한다.
- 모든 논리곱 기호를 생략한다.
- CNF로 변환하기 예
- 술어논리로 변환 전
- 모든 강아지는 포유류이다.
- 바둑이는 강아지이다.
- 바둑이는 포유류이다.
- 모든 포유류는 우유를 생산한다.
- 술어논리로 변환
- ∀x (DOG(x) → MAMMAL(x)).
- DOG(badook).
- MAMMAL(badook).
- ∀x (MAMMAL(x) MILK(x)).
- CNF로 변환
- ¬ DOG(x) ∨ MAMMAL(x)
- DOG(badook).
- MAMMAL(badook).
- ¬ MAMMAL(x) ∨ MILK(x)
- 술어논리로 변환 전
- 도출에 의한 증명
- 증명하고자 하는 사실을 부정하여 절들의 리스트에 추가한다.
- 지식 베이스의 문장들을 CNF 형태로 변환한다.
- 도출할 수 있는 절의 쌍이 더이상 없을 때까지 다음을 반복한다.
- 도출할 수 있는 절의 쌍을 찾아 도출한다.
- 도출절을 절들의 리스트에 추가한다.
- NIL이 유도되면, 증명하고자 하는 사실이 참이다.
- 증명하고자 하는 사실이 거짓이다.
- 도출에 의한 증명 예
- CNF 리스트
- ¬ DOG(x) ∨ MAMMAL(x)
- DOG(badook)
- MAMMAL(badook)
- ¬ MAMMAL(x) ∨ MILK(x)
- 증명하고 싶은 사실
- MILK(badook)
- 증명 과정
- ¬ DOG(x) ∨ MAMMAL(x)
- DOG(badook)
- MAMMAL(badook)
- ¬ MAMMAL(x) ∨ MILK(x)
- ¬ MILK(badook)(부정을 하고 시작한다. 이후 empty clause, NIL이 만들어지면 모순)

- CNF 리스트
8. 프롤로그(prolog)
- 설치 및 실습 준비
- https://www.swi-prolog.org/ 에서 다운로드할 수 있는 SWI-Prolog를 설치해보자.
- parent(Y,X) :- child(X,Y).
- father(Y,X) :- child(X,Y), male(Y).
- 프롤로그에서는 변수를 항상 대문자로 작성해야 한다.
- "father(Y,X) :- child(X,Y), male(Y)."은 "X가 Y의 자식이고 Y가 남성이면 Y는 X의 아버지이다."를 의미한다.
- 즉 child(X,Y) ∧ male(Y) → father(Y,X)을 의미한다.
- 프롤로그의 규칙에서 논리합은 사용하지 않는다. 논리곱만을 사용한다.
- https://www.swi-prolog.org/ 에서 다운로드할 수 있는 SWI-Prolog를 설치해보자.
- 프롤로그에서 사실 입력(Knowledge Base가 된다)
- 상수는 소문자로 입력한다.
- child(son1, kim).
- child(son2, kim).
- male(kim).
- male(son1).
- male(son2).
- 상수는 소문자로 입력한다.
- 프롤로그 실습
- 다음과 같은 문장들을 저장하는 파일 main.pl 을 생성한다.
- child(son1, kim).
- child(son2, kim).
- male(kim).
- male(son1).
- male(son2).
- parent(Y,X) :- child(X,Y).(참, 거짓을 출력한다)
- father(Y,X) :- child(X,Y), male(Y).(참, 거짓을 출력한다)
- [File] -> [Consult...] 메뉴 항목을 선택하여서 main.pl 을 불러들인다.
- 다음과 같은 문장들을 저장하는 파일 main.pl 을 생성한다.
반응형
'AI > 인공지능' 카테고리의 다른 글
| [인공지능]6. 퍼지 논리(Fuzzy Logic) (0) | 2021.10.13 |
|---|---|
| [인공지능]4. 전문가 시스템 (0) | 2021.10.04 |
| [인공지능]3. 게임 트리 (0) | 2021.10.01 |
| [인공지능]2. 탐색 (0) | 2021.09.23 |


