반응형
목차
- 퍼지 논리
- 크리스프 집합과 퍼지 집합
- 퍼지 집합에서의 연산자
- 퍼지 추론
1. 퍼지 논리
퍼지 논리란?
- 퍼지 논리(fuzzy logic)는 명확하게 정의될 수 없는 지식(이진화를 할 수 없는 지식)을 표현하는 방법이다.
- 여기서 주의할 점은 퍼지 논리가 애매한 논리는 아니라는 것이다. 퍼지 논리는 애매함을 다루는 질서정연한 논리이다.
- 흔히 인간은 모호한 단어를 사용하여서 문제를 해결하거나 지식을 표현한다.
이진 논리와 퍼지 논리
- 이진 논리(부울 논리)
- 참과 거짓(1 또는 0) - 흑백 논리
- 예: "80점 이상은 우수한 성적이다." → 만약 79점은 우수하지 않은 성적인가?
- 퍼지 논리
- 0.0에서 1.0까지의 진리값을 가진다.
- 지식 표현의 애매성을 해결할 방법이 필요하여 나왔다.
- 1965년 Zadeh에 의해 퍼지 집합에 관한 이론이 처음 제시되었다.
- 이후 퍼지 명제나 규칙을 다루기 위한 퍼지 논리로 발전되었다.
- 예
- 이진 논리
- 날씨가 춥습니까?
- TRUE 1
- FALSE 0
- 퍼지 논리
- 아주 추움 0.9
- 다소 추움 0.6
- 약간 추움 0.3
- 이진 논리
퍼지 논리를 사용할 수 있는 분야
- 세탁기에서 옷감의 오염도에 따라 세탁 시간을 0.0에서 1.0까지 설정
- 앞차와 가까운지 여부를 근접도로 판단하여 브레이크의 강도를 0.0에서 1.0까지 설정
2. 크리스프 집합과 퍼지 집합
퍼지 논리와 집합
- 명제 논리 == 기존 집합(크리스프 집합)
- 퍼지 논리 == 퍼지 집합
- 소속 함수(Membership Function)
- A = {7, 8, 9}
- μA(x) = {1 if x ∈ A | 0 if x ∉ A}
- μA: A → {0, 1}
크리스프 집합
- 기존의 집합 이론
- 속하든지 그렇지 않다면 속하지 않은 것
- 소속 함수(Membership Function)으로 표현
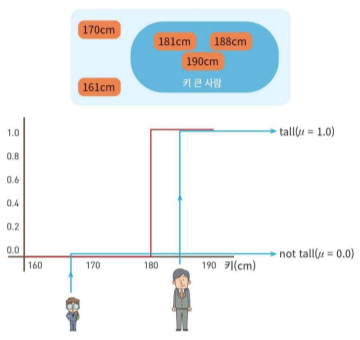
퍼지 집합
- 원소가 집합에 속하는 정도에 따라 소속 함수 값을 0과 1 사이의 값으로 대응
- 예) "키 큰 사람"이라는 집합
- "키 큰 사람" = {0.3/172cm, 0.5/175cm, 0.95/185cm, 1.0/190cm}
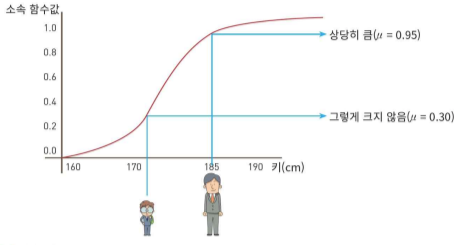
크리스프 집합, 퍼지 집합

퍼지 집합의 표기 방법
- 비연속적인 퍼지 집합
- "키 큰 사람" = {0.30/170cm, 0.50/175cm, 0.95/180cm, 1.0/190cm}
- "키 큰 사람" = {(170cm, 0.3), (175cm, 0.5), (180cm, 0.95), (190cm, 1.0)}
- 연속적인 퍼지 집합
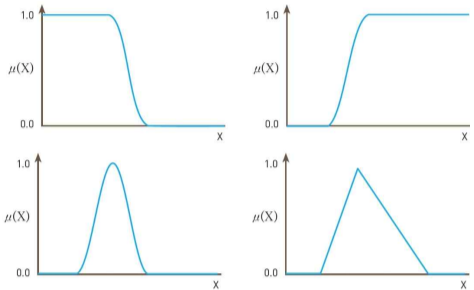
3. 퍼지 집합에서의 연산자
논리 연산자
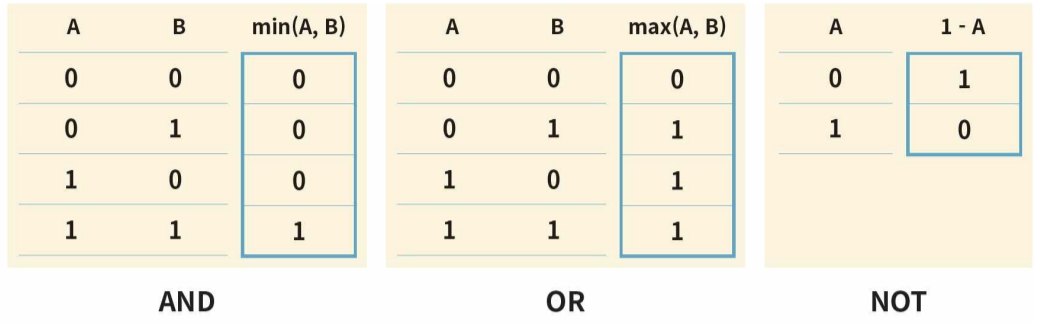
- 퍼지 집합 이론에서도 (NOT), (AND), (OR) 등의 논리 연산자가 있다.
- μ¬A(x) = 1 - μA(x)
- μA∧B(x) = min([μA(x), μB(x)]
- μA∨B(x) = max([μA(x), μB(x)]
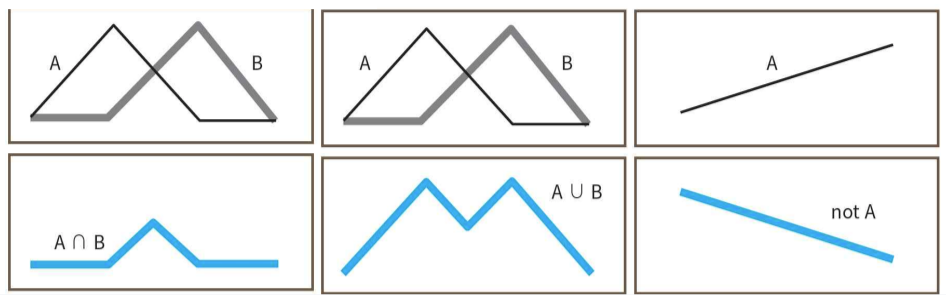
크리스프 집합에서의 AND,OR,NOT와 버그
4. 퍼지 추론
퍼지 추론
- 기존의 추론
- 규칙 #1: IF 온도가 높다. THEN 팬의 속도를 증가시킨다.
- 사실 #1: 온도가 약간 높다.
- -------------------------------------------------------------------------------
- 추론된 사실: ???
- 퍼지 추론
- 규칙 #1: IF 온도가 높다. THEN 팬의 속도를 빠르게 한다.
- 사실 #1: 온도가 약간 높다.
- -------------------------------------------------------------------------------
- 사실 #2: 팬의 속도를 약간 빠르게 한다.
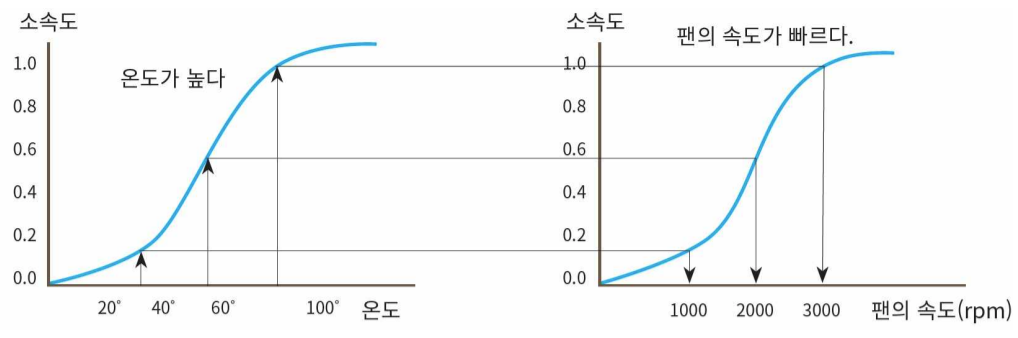
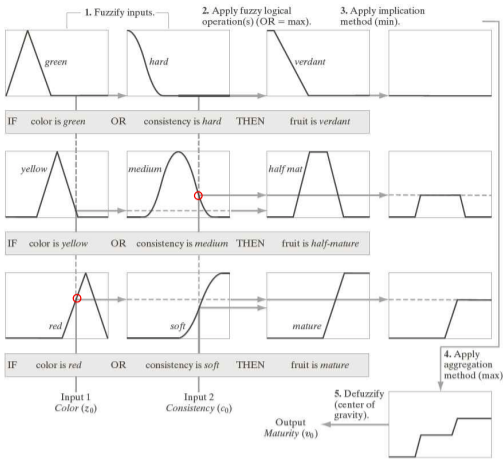
퍼지 추론의 과정
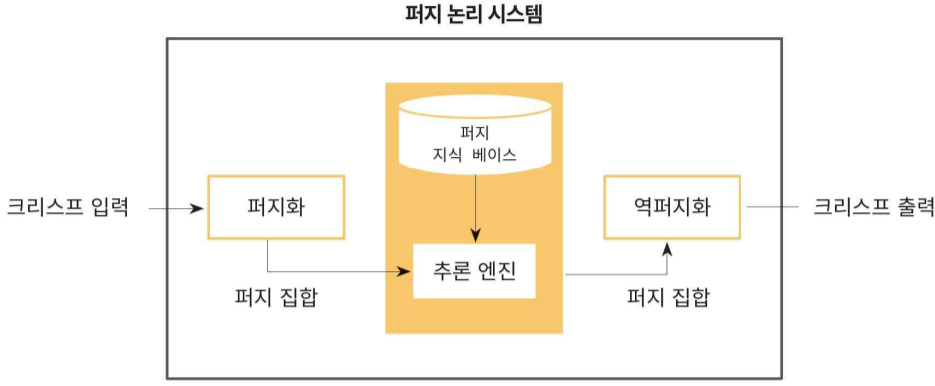
Max-Min추론 방법
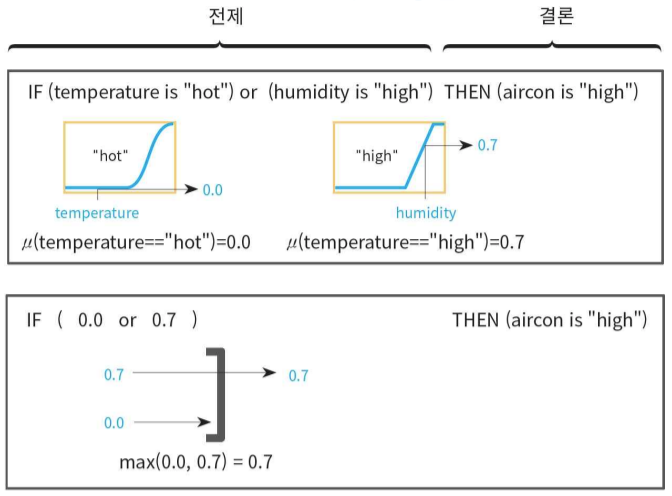
함축 연산자 처리

역 퍼지화
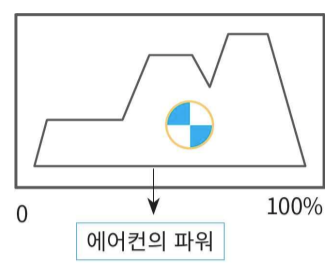
가ㅏ운데 모양은 중심값을 찾아 적용한다는 의미이다.
규칙이 여러 개인 경우
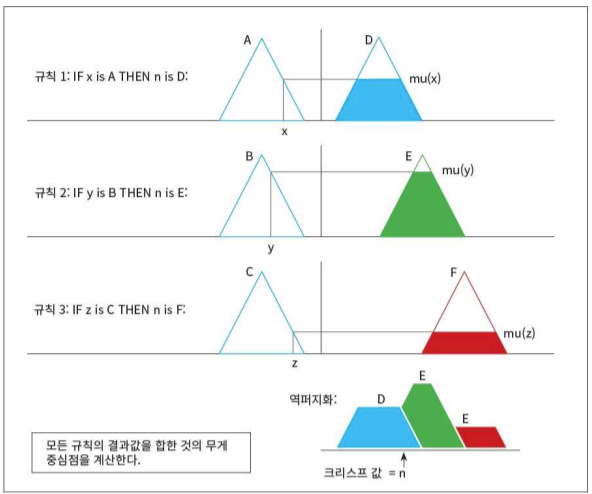
중심값(무게중심) n을 뽑아내 적용하는 것이다.
Process
- Fuzzify the inputs(인풋을 퍼지화한다)
- Perform any required fuzzy logical operations(필요한 퍼지 논리 연산을 진행한다)
- Apply an implication method(함축 연산을 적용한다)
- Apply an aggregation method to the fuzzy set from step(스텝별로 퍼지 집합의 집계 방법을 적용한다)
- Defuzzify the final output fuzzy set(퍼지 집합의 결과를 역퍼지화한다)
반응형
'AI > 인공지능' 카테고리의 다른 글
| [인공지능]5. 지식의 표현(Knowledge Representation) (0) | 2021.10.04 |
|---|---|
| [인공지능]4. 전문가 시스템 (0) | 2021.10.04 |
| [인공지능]3. 게임 트리 (0) | 2021.10.01 |
| [인공지능]2. 탐색 (0) | 2021.09.23 |